Skip to main content

Algorithm

This explanation demonstrates calculations as SQL, but the same principles apply for other implementations.

Setup​

First, I have a table that includes all utilities and subgroups. For this example I’ve create [respdata] and populated it with 100,000 records.

CREATE TABLE [respdata]
(
    [respid] int,

    -- utilities
    [sku1] float,
    [sku2] float,
    [sku3] float,
    [sku4] float,
    [sku5] float,
    [size1] float,
    [size2] float,
    [color1] float,
    [color2] float,
    [color3] float,
    [price1] float,
    [price2] float,

    -- subgroups
    [region] int,
    [gender] int,
    [group1] bit,
    [group2] bit
)
-- populate 100k records of random data
DECLARE @i int = 1;
WHILE @i <= 100000 BEGIN
    INSERT INTO [respdata] 
           ([respid], [sku1], [sku2], [sku3], [sku4], [sku5], [size1], [size2], [color1], [color2], [color3], [price1], [price2], [region],          [gender],          [group1],        [group2]       ) 
    VALUES (@i,       rand(), rand(), rand(), rand(), rand(), rand(),  rand(),  rand(),   rand(),   rand(),   rand(),   rand(),   round(rand()*5,0), round(rand()*2,0), round(rand(),0), round(rand(),0));
    SET @i = @i + 1;
END
note

I'm not creating any indexes yet

Step 1: Exponeniated sum of utilities​

When a user runs a forecast, a query is designed that sums the correct mix of utilities based on input configuration, per respondent.

Consider this example input configuration:

input config

Notice in this query below that we pick only the relevant utilities (i.e. color3 for product p2) and we use only the necessary price utilities for interpolation.

WITH step1 As (
    SELECT
        *
        ,[expSumUtils.p1] = exp(sku1 + size1 + color2 + price1 + price2*0.59)
        ,[expSumUtils.p2] = exp(sku2 + size1 + color3 + price1 + price2*0.59)
        ,[expSumUtils.p3] = exp(sku3 + size1 + color1 + price1 + price2*0.19)
        ,[expSumUtils.p4] = exp(sku4 + size2 + color3 + price1)
        ,[expSumUtils.p5] = exp(sku5 + size2 + color3 + price1 + price2*0.59)
    FROM [respdata]
)

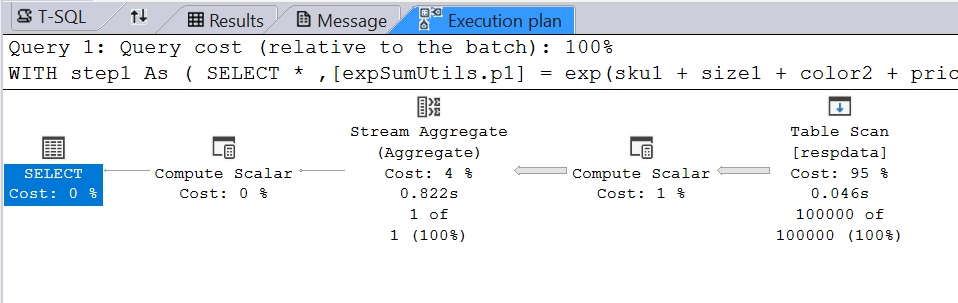
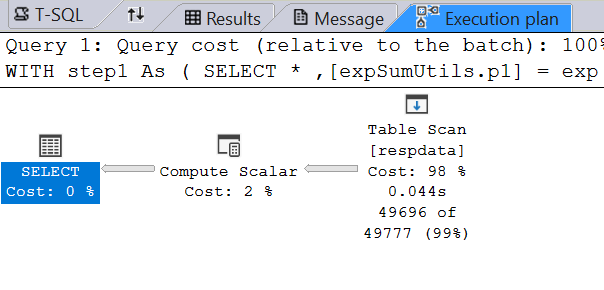
One goal is to keep the calculations at just one table scan since table scans are expensive. The query execution plan for the above uses just one table scan:

execution plan

Step 2: Calculate a sum column​

The share of preference calculation requires a sum of all the expSumUtils. We're naming it [expSumUtils.__sum].

note

The first choice calculation (not shown here) is a little different in that it calculates a max instead of a sum and finds the number of products tied at max.

,step2 AS (
    SELECT
        *
        ,[expSumUtils.__sum] =
            [expSumUtils.p1] +
            [expSumUtils.p2] +
            [expSumUtils.p3] +
            [expSumUtils.p4] +
            [expSumUtils.p5]
    FROM step1
)

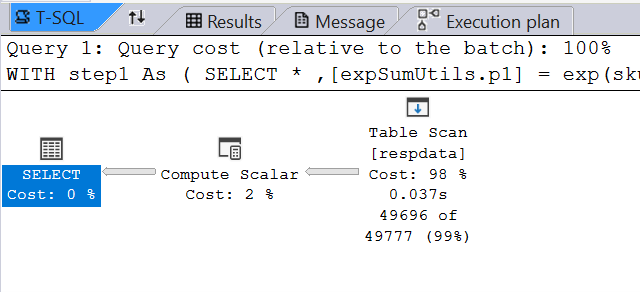
SQL Server optimizes the Common Table Expressions for both step1 and step2 into a single table scan. The execution plan is pretty much identical.

execution plan

Step 3: Calculate individual probabilities (iProbs)​

Individual level probabilities are calculated by dividing [expSumUtils.(product_id)] by [expSumUtils.__sum].

,step3 AS (
    SELECT
        *
        ,[iProb.p1] = [expSumUtils.p1] / [expSumUtils.__sum]
        ,[iProb.p2] = [expSumUtils.p2] / [expSumUtils.__sum]
        ,[iProb.p3] = [expSumUtils.p3] / [expSumUtils.__sum]
        ,[iProb.p4] = [expSumUtils.p4] / [expSumUtils.__sum]
        ,[iProb.p5] = [expSumUtils.p5] / [expSumUtils.__sum]
    from step2
)

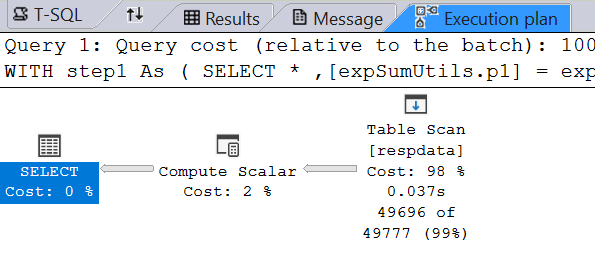
With all three steps combined, we’re still at just one table scan and the same execution plan:

execution plan

Respondent Filtering​

If there exists a universal respondent filter, we’ll want to apply it so that we’re only calculating the individual probabilities for the included respondents. See row 10 highlighted below:

WITH step1 As (
    SELECT
        *
        ,[expSumUtils.p1] = exp(sku1 + size1 + color2 + price1 + price2*0.59)
        ,[expSumUtils.p2] = exp(sku2 + size1 + color3 + price1 + price2*0.59)
        ,[expSumUtils.p3] = exp(sku3 + size1 + color1 + price1 + price2*0.19)
        ,[expSumUtils.p4] = exp(sku4 + size2 + color3 + price1)
        ,[expSumUtils.p5] = exp(sku5 + size2 + color3 + price1 + price2*0.59)
    FROM respdata
    WHERE gender=1
)
,step2 AS (
    SELECT
        *
        ,[expSumUtils.__sum] =
            [expSumUtils.p1] +
            [expSumUtils.p2] +
            [expSumUtils.p3] +
            [expSumUtils.p4] +
            [expSumUtils.p5]
    FROM step1
)
,step3 AS (
    SELECT
        *
        ,[iProb.p1] = [expSumUtils.p1] / [expSumUtils.__sum]
        ,[iProb.p2] = [expSumUtils.p2] / [expSumUtils.__sum]
        ,[iProb.p3] = [expSumUtils.p3] / [expSumUtils.__sum]
        ,[iProb.p4] = [expSumUtils.p4] / [expSumUtils.__sum]
        ,[iProb.p5] = [expSumUtils.p5] / [expSumUtils.__sum]
    from step2
)
select * from step3

  This is where an Index will come in handy and improve record seek time.

Without index:​

execution plan

CREATE INDEX idx_gender ON respdata (gender) 
INCLUDE (
    [respid], [sku1], [sku2], [sku3], [sku4], [sku5],
    [size1], [size2], [color1], [color2], [color3],
    [price1], [price2], [region], [group1], [group2]
)

With index (improved speed):​

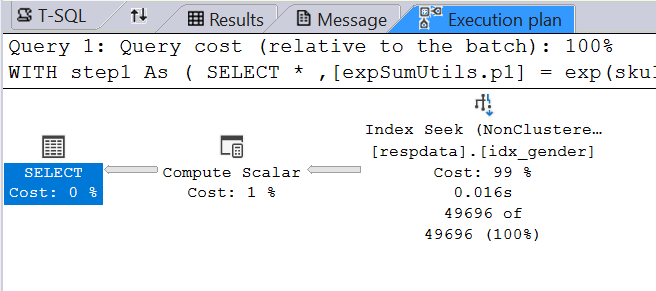
execution plan

note

I’m removing the index and respondent filter for the rest of the documentation.

Step 4: Aggregate iProbs​

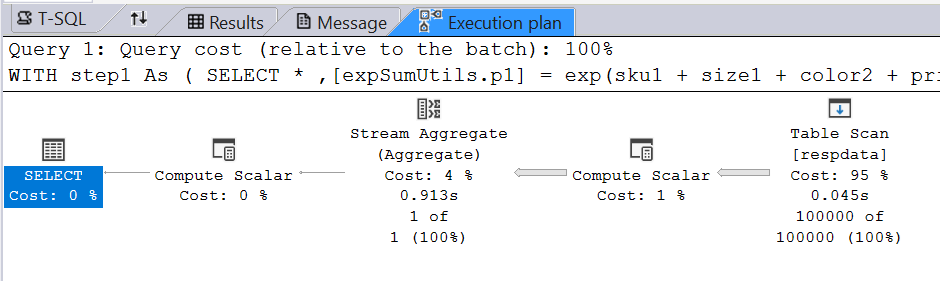
We calculate the share as an average of the individual probabilities.

,aggregate1 AS (
    SELECT
        [share.p1] = avg([iProb.p1]),
        [share.p2] = avg([iProb.p2]),
        [share.p3] = avg([iProb.p3]),
        [share.p4] = avg([iProb.p4]),
        [share.p5] = avg([iProb.p5]),
        [n] = count(*)
    FROM step3
)

The result is a single row with a share for each product:

results

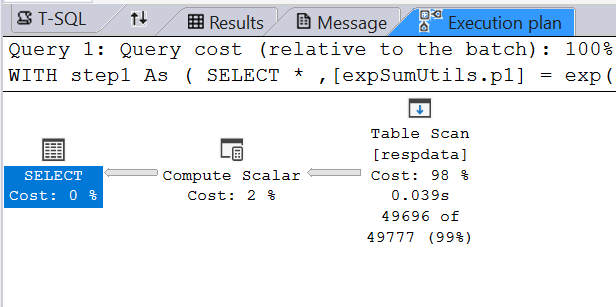
The query execution now includes an aggregation stream.

Execution Plan

Step 4 (Alt): Aggregation with comparison groups​

If comparison groups are present, we include them in aggregation.

,aggregate1 AS (
    SELECT
        -- group1
        [share.p1.group1] = avg(CASE when group1=1 then [iProb.p1] else null END),
        [share.p2.group1] = avg(CASE when group1=1 then [iProb.p2] else null END),
        [share.p3.group1] = avg(CASE when group1=1 then [iProb.p3] else null END),
        [share.p4.group1] = avg(CASE when group1=1 then [iProb.p4] else null END),
        [share.p5.group1] = avg(CASE when group1=1 then [iProb.p5] else null END),
        [n.group1] = count(CASE when group1=1 then 1 else null end),

        -- group2
        [share.p1.group2] = avg(CASE when group2=1 then [iProb.p1] else null END),
        [share.p2.group2] = avg(CASE when group2=1 then [iProb.p2] else null END),
        [share.p3.group2] = avg(CASE when group2=1 then [iProb.p3] else null END),
        [share.p4.group2] = avg(CASE when group2=1 then [iProb.p4] else null END),
        [share.p5.group2] = avg(CASE when group2=1 then [iProb.p5] else null END),
        [n.group2] = count(CASE when group2=1 then 1 else null end)
    FROM step3
)
note

Another way to break the results out by group is to use the GROUP BY expression. Sometimes I’ll also use a hybrid of GROUP BY and the CASE statements above. But for this explanation I’m keeping things simple.

The result is still a single row, but with a share of each product by each group.

Results

  The execution plan is still the same but probably uses a bit more memory and takes a little longer:

Execution Plan